剑指offer

所有题按照leetcode

JZ3 数组中重复数字

数组中重复的数字

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

1
2
3

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3

1.遍历数组

Set<Integer> set = new HashSet<>();
int repeat = -1;
for (int num : nums) {
    if (!set.add(num)){
        repeat = num;
        break;
    }
}
return repeat;

2.先排序在查找

public int findRepeatNumber(int[] nums) {
    Arrays.sort(nums);
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] == nums[i - 1])
            return nums[i];
    }
    return -1;
}

3.空间换时间

public int findRepeatNumber(int[] nums) {
    int[] arr = new int[nums.length];
    for(int i = 0; i < nums.length; i++){
        arr[nums[i]]++;
        if(arr[nums[i]] > 1) return nums[i];
    }
    return -1;
}

JZ4 二维数组的查找

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解题思路

该二维数组中的一个数，小于它的数一定在其左边，大于它的数一定在其下边。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

public class JZ1 {
    public boolean Find(int target, int [][] array) {
        if (array == null || array.length == 0 || array[0].length == 0 )
            return false;
        int row = array.length; //行
        int col = array[0].length ;//列
        //从右上角开始
        int r = 0, c = col-1;  //r表示那一行，c表示那一列
        while (r <= row-1 && c >= 0){
            if (target == array[r][c]){
                return true;
            }else if ( target < array[r][c]){
                c--;
            }else {
                r++;
            }
        }
        return false;
    }
}

JZ5 替换空格

请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

public class JZ2 {
    public String replaceSpace(StringBuffer str) {
        return str.toString().replace(" ", "%20");
    }
}

JZ6 输入一个链表，按链表从尾到头的顺序返回一个ArrayList

输入一个链表，按链表从尾到头的顺序返回一个ArrayList。

1.递归

public int[]  reversePrint(ListNode head) {
    ArrayList<Integer> ret = new ArrayList<>();
    if (head != null){
        ret = printListFromTailToHead(head.next);
    }
    int res[] = new int[ret.size()];
    for (int i = 0;i<ret.size();i++){
        res[i] = ret.get(i);
    }
    return res;
}
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
    ArrayList<Integer> ret = new ArrayList<>();
    if (listNode != null){
        ret.addAll(printListFromTailToHead(listNode.next));
        ret.add(listNode.val);
    }
    return ret;
}

2.栈

public int[] reversePrint(ListNode head) {
    Stack<ListNode> stack = new Stack<>();
    ListNode temp = head;
    while (temp != null) {
        stack.push(temp);
        temp = temp.next;
    }
    int size = stack.size();
    int[] res = new int[size];
    for (int i = 0; i < size; i++) {
        res[i] = stack.pop().val;
    }
    return res;
}

3.不用栈也不用递归

先遍历获取长度，得到数组，在从最后开始赋值

public static int[] reversePrint3(ListNode head) {
    ListNode node = head;
    int count = 0;
    while (node != null) {
        ++count;
        node = node.next;
    }
    int[] nums = new int[count];
    node = head;
    for (int i = count - 1; i >= 0; --i) {
        nums[i] = node.val;
        node = node.next;
    }
    return nums;
}

JZ7 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

递归

前序遍历的第一个值为根节点的值，使用这个值将中序遍历结果分成两部分，左部分为树的左子树中序遍历结果，右部分为树的右子树中序遍历的结果。然后分别对左右子树递归地求解。

前序遍历的首个元素即为根节点 root 的值；
在中序遍历中搜索根节点 root 的索引，可将中序遍历划分为 [ 左子树 | 根节点 | 右子树 ] 。
根据中序遍历中的左（右）子树的节点数量，可将前序遍历划分为 [ 根节点 | 左子树 | 右子树 ] 。

左子树：根节点索引为 pre_root + 1 ，中序遍历的左右边界分别为 in_left 和 i - 1。
右子树：根节点索引为pre_root+i-in_left+1（即：根节点索引 + 左子树长度 + 1），中序遍历的左右边界分别为 i + 1 和 in_right。

HashMap<Integer,Integer> dic = new HashMap<>();//保存中序遍历
int []po;
public  TreeNode buildTree(int[] pre, int[] in) {
    if (pre == null || pre.length == 0) return null;
    po=pre;
    //放入中序遍历的节点
    for (int i = 0;i<in.length;i++){
        dic.put(in[i],i);
    }
    return recur(0,0,in.length-1);
}
public TreeNode recur(int pre_root,int in_left ,int in_right){
    if (in_left>in_right) return null;//不存在

    TreeNode root = new TreeNode(po[pre_root]);
    int i = dic.get(po[pre_root]);//分为2半
    root.left = recur(pre_root+1,in_left,i-1);
    root.right = recur(pre_root+i-in_left+1,i+1,in_right);
    return root;

}

public static void main(String[] args) {
   int pre[] = {3,9,20,15,7};
   int in[] = {9,3,15,20,7};
   new JZ7().buildTree(pre, in);
}

栈

前序遍历挨着的两个值比如m和n，他们会有下面两种情况之一的关系。

1，n是m左子树节点的值。

2，n是m右子树节点的值或者是m某个祖先节点的右节点的值。

对于第一个知识点我们很容易理解，如果m的左子树不为空，那么n就是m左子树节点的值。

对于第二个问题，如果一个结点没有左子树只有右子树，那么n就是m右子树节点的值，如果一个结点既没有左子树也没有右子树，那么n就是m某个祖先节点的右节点，我们只要找到这个祖先节点就好办了。

public  TreeNode buildTree2(int[] pre, int[] in) {
    if (pre == null || pre.length == 0) return null;
    Stack<TreeNode> s = new Stack<>();
    //创建根节点
    TreeNode root = new TreeNode(pre[0]);
    TreeNode cur = root;

    for (int i = 1,j = 0;i<pre.length;i++){
        if (cur.val != in[j]){ //第一种情况
            cur.left = new TreeNode(pre[i]);
            s.push(cur);
            cur = cur.left;
        }else {  //第二种情况
            j++;
            //找到合适的cur，每个子树都出战，直到找到合适的。
            while (!s.isEmpty() &&s.peek().val == in[j]){
                cur = s.pop();
                j++;
            }
            //给cur添加右节点
            cur = cur.right = new TreeNode(pre[i]);
        }
    }

    return root;
}

JZ9 两个栈来实现一个队列

用两个栈来实现一个队列，完成队列的Push和Pop操作。队列中的元素为int类型。

public class JZ5 {
    Stack<Integer> stack1 = new Stack<Integer>();  //in
    Stack<Integer> stack2 = new Stack<Integer>();  //out

    public void push(int node) {
        stack1.push(node);
    }

    public void inToOut(){
        if (stack2.isEmpty()){   //必须stack2出栈完成后才能继续进栈
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
    }

    public int pop() throws Exception {
        inToOut();
        if (stack2.isEmpty()){
            throw new Exception("queue is empty");
        }
        return stack2.pop();
    }
}

JZ10-1 斐波那契数列

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

非递归

public class ZJ10 {
    public int fib(int n) {
        int constant = 1000000007;
        List<Integer> list = new ArrayList<>();
        list.add(0);
        list.add(1);
        for (int i = 2;i<=n;i++){
            int res = list.get(i-1)+list.get(i-2);
            if (res >= constant)
                res = res - constant;
            list.add(res);
        }
        return list.get(n);
    }
}

JZ10-2 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

青蛙可从低一阶的台阶上，也可以从低2阶的台阶上去

public class ZJ10_2 {
    public int numWays(int n) {
        if (n <= 1)
            return 1;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            if (dp[i]>1000000007){
                dp[i] -= 1000000007;
            }
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

JZ11 旋转数组的最小值

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

遍历数组

int min = numbers[0];
for (int i = 1; i < numbers.length; i++) {
    if (min > numbers[i])
        min = numbers[i];
}
return min;

二分法查找

public int minArray2(int[] numbers) {
    int left = 0,right = numbers.length-1;
    while (left < right){
        int mid = left + (right - left) / 2;

        if (numbers[mid] > numbers[right]){ //如果中间值大于最右边的值，说明旋转之后最小的数字肯定在mid的右边
            left = mid +1;
        }else if (numbers[mid]<numbers[left]){ //中间数比左边小
            right = mid;
        }else {
            //如果中间值等于最后一个元素的值，我们是没法确定最小值是
            // 在mid的前面还是后面，但我们可以缩小查找范围，让right
            // 减1，因为即使right指向的是最小值，但因为他的值和mid
            // 指向的一样，我们这里并没有排除mid，所以结果是不会有影响的。
            //比如[3，1，3，3，3，3，3]和[3，3，3，3，3，1，3],中间的值
            //等于最右边的值，但我们没法确定最小值是在左边还是右边
            right--;
        }
    }
    return numbers[right];
}

JZ12 矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的3×4的矩阵中包含一条字符串“bfce”的路径（路径中的字母用加粗标出）。

[[“a”,”b”,”c”,”e”],
[“s”,”f”,”c”,”s”],
[“a”,”d”,”e”,”e”]]

但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

回溯算法

遍历数组，有4个方向的走法。

public boolean exist(char[][] board, String word) {
    char[] words = word.toCharArray();

    for (int i = 0;i<board.length;i++){
        for (int j =0;j<board[0].length;j++){
            if (dfs(board,words,i,j,0)){
                return true;
            }
        }
    }
    return false;
}

/**
 *
 * @param board
 * @param words
 * @param i  座标
 * @param j
 * @param index  到字符串第几个了
 * @return
 */
public boolean dfs(char[][] board,char[] words,int i,int j,int index){
    if (i > board.length-1 || i<0 || j > board[0].length-1 || j<0 || board[i][j] != words[index]){
        return false;
    }
    //已经完成
    if (index == words.length-1){
        return true;
    }
    char tmp = board[i][j]; //保存这个值
    board[i][j] = '/'; //将这个值置位
    //四种走法
    boolean res = dfs(board, words, i + 1, j, index + 1) || dfs(board, words, i - 1, j, index + 1) ||
            dfs(board, words, i, j + 1, index + 1) || dfs(board, words, i , j - 1, index + 1);
    board[i][j]= tmp;

    return res;
}

也可以使用一个另外的数组来记录是否已经被访问。

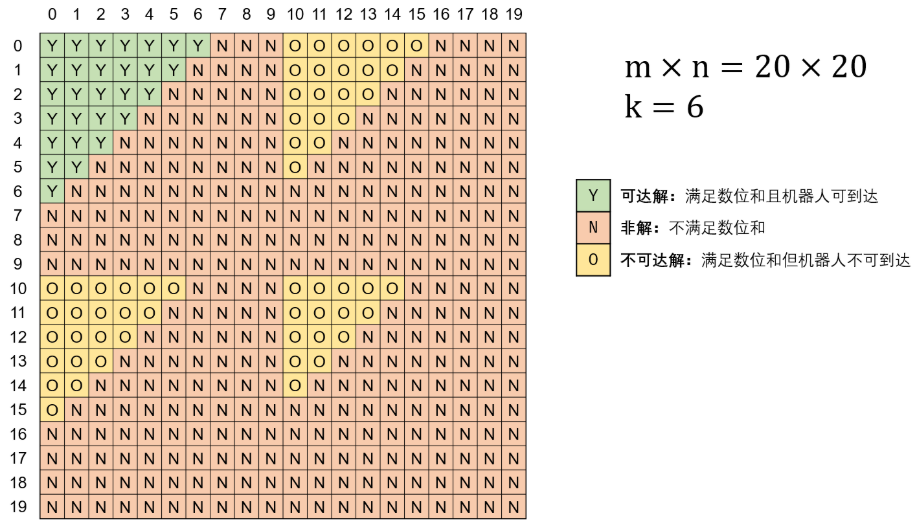
JZ13 机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

使用深度优先搜索（Depth First Search，DFS）方法进行求解。

结论：根据可达解的结构，易推出机器人可仅通过向右和向下移动，访问所有可达解。

public int movingCount(int m, int n, int k) {
    boolean[][] visited = new boolean[m][n];
    return dfs(0, 0, m, n, k, visited);
}

/**
 *
 * @param i
 * @param j
 * @param m
 * @param n
 * @param k
 * @param visited
 * @return
 */
private int dfs(int i, int j, int m, int n, int k, boolean visited[][]){
    //判断出界， 判断这个位置的值有没有超过k,这个位置有没有访问过
    if (i < 0 || i >= m || j < 0 || j >= n || (i/10 + i%10 + j/10 + j%10) > k || visited[i][j]) {
        return 0;
    }
    visited[i][j] = true;
    //计算2个方法走的总和
    return  dfs(i + 1, j, m, n, k, visited)+dfs(i, j + 1, m, n, k, visited)+1;

}

JZ14-1 剪绳子

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

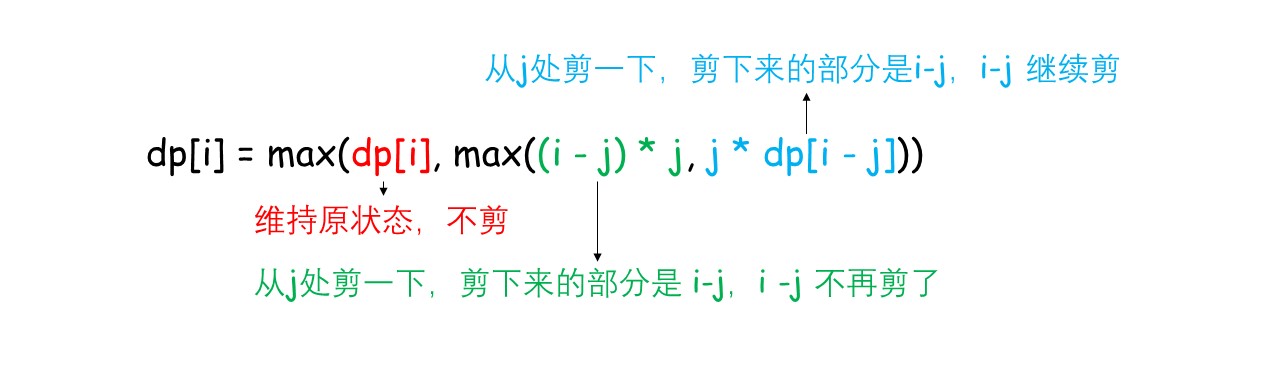
动态规划

建立一维动态数组 dp：

边界条件：dp[1] = dp[2] = 1，表示长度为 2 的绳子最大乘积为 1；
状态转移方程：dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j]))，可以这样理解：

public int cuttingRope(int n) {
    if(n <= 3) return n - 1;
    int[] dp = new int[n + 1];//新建一个动态规划的数组
    /*真正的dp[1] = 0,dp[2] = 1,dp[3] = 2
    但是当n=4时，4=2+2 2*2=4 而dp[2]=1是不对的
            也就是说当n=1/2/3时，分割后反而比没分割的值要小，当大问题用到dp[j]时，说明已经分成了一个j一个i-j，这两部分又可以再分，但是再分不能比他本身没分割的要小，如果分了更小还不如不分
    所以在这里指定大问题用到的dp[1],dp[2],dp[3]是他本身
    */
    dp[2] = 2;
    dp[3] = 3;
    for (int i = 4;i <= n;i++){ //计算每一个
        for(int j= 2;j<=i/2;j++){
            dp[i] = Math.max(dp[i],dp[i-j]*dp[j]); //判断哪个分割值最大
        }
    }
    return dp[n];
}

JZ14-2 剪绳子2

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

贪心算法

认为一份为3是最大的

public int cuttingRope(int n) {
    if(n <= 3) return n - 1;

    long res = 1;
    int p=(int)1e9+7;
    //贪心算法
    while (n>4){
        res = res*3%p;
        n -= 3; //认为3是最大的
    }
    //循环结果有3中 n=2 n=3 n=4
    return (int) (res*n%p);
}

JZ15 二进制中1的个数

请实现一个函数，输入一个整数，输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。

与运算

根据与运算定义，设二进制数字 n ，则有：
若 n & 1 = 0，则 n 二进制最右一位为 00 ；
若 n & 1 = 1 ，则 n 二进制最右一位为 11 。

public class JZ15 {
    public int hammingWeight(int n) {
      int res = 0;
      while (n != 0){
          res +=  n&1; //与运输
          n >>>= 1;
      }
      return res;
    }
}

JZ16 数值的整次方

实现函数double Power(double base, int exponent)，求base的exponent次方。不得使用库函数，同时不需要考虑大数问题。

我的写法

public double myPow(double x, int n) {
    if (x == 1){
        return 1;
    }
    double res = 1;
    if (n>1){
        for(int i = 0; i < n; i++){
            res *= x;
        }
    }else if (n < 0){
        double temp = 1 / x;
        for (int i = 0;i< Math.abs(n) ;i++){
            res *= temp;
        }

    }else if (n == 0){
        res = 1;
    }else {
        res = x;
    }
    return res;
}

2.00000 -2147483648 结果为0

因为int的取值范围是-2147483648到2147483647…所以java的Math.abs(n)在这个时候返回的还是-2147483648

递归求解

使用long类型不会溢出

public double myPow(double x, int n) {
    // 特判，也可以认为是递归终止条件
    long N = n;
    if (N < 0) {
        return 1 / myPow(x, -N);
    }
    return myPow(x, N);
}

private double myPow(double x, long n) {
    if (n == 0) {
        return 1;
    }

    if (x == 1) {
        return 1;
    }

    // 根据指数是奇数还是偶数进行分类讨论
    // 使用位运算的 与 运算符代替了求余数运算

    if ((n % 2) == 0) {
        // 分治思想：分
        double square = myPow(x, n / 2);
        // 分治思想：合，下面同理
        return square * square;
    } else {
        // 是奇数的时候
        double square = myPow(x, (n - 1) / 2);
        return square * square * x;
    }
}

非递归

public double myPow(double x, int n) {
    long N = n;
    if (N < 0) {
        x = 1 / x;
        N *= -1;
    }

    double res = 1;
    while (N > 0) {
        if ((N % 2) == 1) {
            res *= x;
        }

        x *= x;
        N /= 2;
    }
    return res;
}
。

JZ17 从 11 至最大的 n位数的列表

题目要求打印 “从 11 至最大的 n位数的列表” ，因此需考虑以下两个问题

public int[] printNumbers(int n) {
    int end = (int) Math.pow(10,n)-1;
    int res[] = new int[end];
    for(int i = 0; i <end  ; i++){
        res[i] = i+1;
    }
    return res;
}

实际上

由于存在大数问题，结果不能放入int数组中，故这里采用剑指offer原题的直接打印输出的模式。
increment函数，若发生进位则一直进行for循环，直到不产生进位则break。如果i为0（即到了最高位）还发生了进位，则设置isOverflow为true，并返回至主函数的while判断。

public void printNumbers(int n) {
    StringBuilder str = new StringBuilder();
    // 将str初始化为n个'0'字符组成的字符串
    for (int i = 0; i < n; i++) {
        str.append('0');
    }
    while(!increment(str)){
        // 去掉左侧的0
        int index = 0;
        while (index < str.length() && str.charAt(index) == '0'){
            index++;
        }
        System.out.println(str.toString().substring(index));
    }
}
public boolean increment(StringBuilder str) {
    boolean isOverflow = false;
    for (int i = str.length() - 1; i >= 0; i--) {
        char s = (char)(str.charAt(i) + 1);
        // 如果s大于'9'则发生进位
        if (s > '9') {
            str.replace(i, i + 1, "0");
            if (i == 0) {
                isOverflow = true;
            }
        }
        // 没发生进位则跳出for循环
        else {
            str.replace(i, i + 1, String.valueOf(s));
            break;
        }
    }
    return isOverflow;
}

JZ18 删除链表的节点

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

示例 1:
输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

示例 2:
输入: head = [4,5,1,9], val = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

public ListNode deleteNode(ListNode head, int val) {
    ListNode p = head;
    if (p.val == val){
        return p.next;
    }

    ListNode q = p;
    p = p.next;

    while ( p!=null ){

        if (p.val == val){
            q.next = p.next;
            break;
        }
        q=p;
        p = p.next;
    }
    return head;

}

本题中，输入的类型为：head: ListNode, val: int，即 val 的类型是整形；
在《剑指offer》中，默认输入为 head: ListNode, val: ListNode，即 val 的类型是链表。

假如 head 为 4 -> 5 -> 1 -> 9，val 为 5 -> 1 -> 9，表示我们要删除结点 5，这时我们使用信息交换，把 val 改为 1 -> 9的信息就行了。

为什么呢？因为我们把待删除节点的后一个元素赋值给待删除节点，也就相当于删除了当前元素。

但是聪明的你一定会举出反例：如果 val 的值是最后一个元素 9 呢？我们无法找到 9 的后一个元素（因为没有），只能重头开始找待删除元素 9，这样的话时间复杂度再次变成了 O(N)。

//这个不通过，仅供参考
public static ListNode deleteNode(ListNode head, ListNode val){
    if (head == null || val == null){
        return null;
    }
    if (val.next != null){   // 待删除节点不是尾节点
        ListNode next = val.next;
        val.val = next.val;
        val.next = next.next;
    } else if (head == val){   // 待删除节点只有一个节点，此节点为头节点
        head = null;
    } else {   // 待删除节点为尾节点
        ListNode cur = head;
        while (cur.next != val){
            cur = cur.next;
        }
        cur.next = null;
    }
    return head;
}

JZ19 正则表达式匹配

请实现一个函数用来匹配包含’. ‘和’ * ‘的正则表达式。模式中的字符’.’表示任意一个字符，而’ * ‘表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa”与模式”a.a”和”abaca”匹配，但与”aa.a”和”ab*a”均不匹配。

示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

JZ21 调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

1
2
3

输入：nums = [1,2,3,4]
输出：[1,3,2,4] 
注：[3,1,2,4] 也是正确的答案之一。

我的思路类似于快速排序

从两边开始查找

public int[] exchange(int[] nums) {

        int l = 0,r = nums.length-1,temp;
        while (l<r){
             while (l<r && (nums[l]&1) == 1){
                l++;
            }
            while (l<r && (nums[r]&1) == 0){
                r--;
            }
            if (l<r){
                temp = nums[l];
                nums[l] = nums[r];
                nums[r] = temp;
            }

        }
        return nums;
    }

JZ22 链表中倒数第k个节点

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有6个节点，从头节点开始，它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。

public ListNode getKthFromEnd(ListNode head, int k) {
    ListNode pre = head , tail = head;
    int i = 0;
    while (tail.next!=null){
        tail = tail.next;
        i++;
    }
    while (i >= k){
        pre = pre .next;
        i--;
    }
    return pre;
}

快慢指针

public ListNode getKthFromEnd2(ListNode head, int k) {
    ListNode pre = head, tail = head;
    while (tail != null && k > 0) {

        tail = tail.next;
        k--;
    }

    while (tail != null) {

        pre = pre.next;
        tail = tail.next;
    }

    return pre;
}

JZ24 反转链表

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

头插法

public ListNode reverseList(ListNode head) {
    ListNode newhead = new ListNode(0);

    while (head != null){
        ListNode node = head.next;
        head.next = newhead.next;
        newhead.next = head;
        head = node ;
    }
    return newhead.next;
}

递归

public ListNode reverseList2(ListNode head) {
    if (head == null || head.next == null){
        return head;
    }
    ListNode node = head.next;
    ListNode newhead = reverseList2(node); //递归
    node.next = head;  //反转
    head.next = null;
    return newhead;
}

JZ25 合并两个有序节点

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

1 2	输入：1->2->4, 1->3->4 输出：1->1->2->3->4->4

迭代

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode head = new ListNode(0);
    ListNode node = head;
    while (l1!=null && l2 != null){
        if (l1.val<l2.val){
            node.next = l1;
            l1 = l1.next;
        }else {
            node.next = l2;
            l2 = l2.next;
        }
        node = node.next;
    }
    if (l1!=null){
        node.next = l1;
    }
    if (l2!=null){
        node.next = l2;
    }

    return head.next;
}

递归

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    if (l1 == null){
        return l2;
    }
    if (l2 == null){
        return l1;
    }

    if (l1.val<l2.val){
        l1.next = mergeTwoLists(l1.next,l2);
        return l1;
    }else {
        l2.next = mergeTwoLists(l1,l2.next);
        return l2;
    }
}

JZ26 树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构，即 A中有出现和B相同的结构和节点值。

例如:

给定的树 A:
     3
    / \
   4   5
  / \
 1   2
给定的树 B：
   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

解题思路：

若树 B 是树 A 的子结构，则子结构的根节点可能为树 AA的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

先序遍历树 A 中的每个节点 nA ；（对应函数 isSubStructure(A, B)）
判断树 A 中以 nA 为根节点的子树是否包含树 B 。（对应函数 recur(A, B)）

//找到A节点和B节点值相同的
public boolean isSubStructure(TreeNode A, TreeNode B) {
    if (B == null || A == null){
        return false;
    }
    if (A.val == B.val && recur(A,B)){
        return true;
    }
    return isSubStructure(A.left,B) || isSubStructure(A.right,B);
}
//判断A树是不是B树的子树
private boolean recur(TreeNode a, TreeNode b) {
    //b为null说明b已经匹配完成
    if (b == null){
        return true;
    }
    //a树为null 或节点值不相等说明匹配失败
    if (a == null || a.val!=b.val){
        return false;
    }
    return recur(a.left,b.left) && recur(a.right,b.right);
}

JZ27 二叉树镜像

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

使用递归的方式

public class JZ27 {
    public TreeNode mirrorTree(TreeNode root) {

        if (root == null){
            return null;
        }

        TreeNode temp = root.left;
        root.left =  mirrorTree(root.right);
        root.right = mirrorTree(temp);

        return root;
    }
}

辅助栈

特例处理：当 root 为空时，直接返回 null ；
初始化：栈（或队列），本文用栈，并加入根节点 root。
循环交换：当栈 stack 为空时跳出；
1. 出栈：记为 node ；
2. 添加子节点：将 node 左和右子节点入栈；
3. 交换：交换 node 的左 / 右子节点。
返回值：返回根节点 root 。

public TreeNode mirrorTree2(TreeNode root) {

    if (root == null){
        return null;
    }
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    //循环交换
    while (!stack.isEmpty()){
        TreeNode node = stack.pop();
        if(node.left != null) stack.add(node.left);
        if(node.right != null) stack.add(node.right);
        TreeNode tmp = node.left;
        node.left = node.right;
        node.right = tmp;
    }
    return root;
}

JZ28 对称的二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

解题思路：
对称二叉树定义：对于树中任意两个对称节点 L 和 R ，一定有：

L.val = R.val ：即此两对称节点值相等。
L.left.val = R.right.val：即 L 的左子节点和 R的右子节点对称；
L.right.val = R.left.val：即 L 的右子节点和 R的左子节点对称。

isSymmetric(root) ：

特例处理：若根节点 root 为空，则直接返回 true。
返回值：即 recur(root.left, root.right) ;

recur(L, R) ：

终止条件：

当 L 和 R 同时越过叶节点：此树从顶至底的节点都对称，因此返回 true；
当 L 或 R 中只有一个越过叶节点：此树不对称，因此返回 false；
当节点 L值 ≠节点 R 值：此树不对称，因此返回 false ；

递推工作：

判断两节点 L.left 和 R.right是否对称，即 recur(L.left, R.right) ；
判断两节点 L.right和 R.left是否对称，即 recur(L.right, R.left) ；
返回值：两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。

public boolean isSymmetric(TreeNode root) {
    if(root == null) return true;
    return recur(root.left,root.right);
}

private boolean recur(TreeNode left, TreeNode right) {

    if (left == null && right == null){
        return true;
    }
    if (left == null || right == null || left.val!= right.val){
        return false;
    }
    return recur(left.left,right.right) && recur(left.right,right.left);
}

JZ29 顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

解题思路：

根据题目示例 matrix = [[1,2,3],[4,5,6],[7,8,9]] 的对应输出 [1,2,3,6,9,8,7,4,5] 可以发现，顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。

算法流程：

空值处理：当 matrix 为空时，直接返回空列表 [] 即可。
初始化：矩阵左、右、上、下四个边界 l , r , t , b ，用于打印的结果列表 res 。
循环打印： “从左向右、从上向下、从右向左、从下向上” 四个方向循环，每个方向打印中做以下三件事（各方向的具体信息见下表）；
1. 根据边界打印，即将元素按顺序添加至列表 res 尾部；
2. 边界向内收缩 1 （代表已被打印）；
3. 判断是否打印完毕（边界是否相遇），若打印完毕则跳出。
返回值：返回 res 即可。

打印方向	1. 根据边界打印	2. 边界向内收缩	3. 是否打印完毕
从左向右	左边界l ，右边界 r	上边界 t 加 1	是否 t > b
从上向下	上边界 t ，下边界b	右边界 r 减 1	是否 l > r
从右向左	右边界 r ，左边界l	下边界 b 减 1	是否 t > b
从下向上	下边界 b ，上边界t 1	左边界 l 加 1	是否 l > r

public class JZ29 {
    public int[] spiralOrder(int[][] matrix) {
        if (matrix.length == 0){
            return new int[0];
        }
        int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1, x = 0;
        int[] res = new int[(r + 1) * (b + 1)];
        while (true){
            //横向向左
            for(int i = l; i <=r ; i++){
                res[x++] = matrix[t][i];
            }
            if (++t > b) break;
            //竖向向下
            for(int i = t; i <= b ; i++){
                res[x++] = matrix[i][r];
            }
            if (--r < l) break;
            //横向向右
            for(int i = r; i >= l; i--){
                res[x++] = matrix[b][i];
            }
            if (--b < t) break;

            for(int i = b; i >=t ; i--){
                res[x++] = matrix[i][l];
            }
            if (++l > r) break;
        }
        return res;
    }
}

JZ30 包含min函数的栈

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

使用2个栈，一个存放数据，一个存放最小值

public class JZ30 {
    /** initialize your data structure here. */
    Stack<Integer> stack , min;

    public JZ30() {
        stack = new Stack<Integer>();
        min = new Stack<Integer>();
    }

    public void push(int x) {
        stack.push(x);
        if (min.empty() || x <= min()){
            min.push(x);
        }
    }

    public void pop() {
        //如果出栈的值等于最小值，说明栈中的最小值
        //已经出栈了，因为min中的栈顶元素存放的
        //就是最小值，所以stack2栈顶元素也要出栈
        if (stack.pop() == min()){
            min.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int min() {
        return min.peek();
    }
}

JZ31 栈的弹出压入

public class JZ31 {
    /*
    遍历push放入栈中，
    遍历压栈序列，循环弹出
    如果这个栈是正确的流程,栈就为空
     */
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        for (int num:pushed){
            stack.push(num);
            while (!stack.isEmpty() && stack.peek() == popped[i]){ //模拟栈的出栈顺序
                stack.pop();
                i++;
            }
        }
        return stack.isEmpty();
    }
}

JZ32 从上到下打印二叉树

1.

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

//用队列控制
public int[] levelOrder(TreeNode root) {
    if (root == null) return new int[0];
    List<Integer> list = new ArrayList<>();
    LinkedList<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        TreeNode node = queue.poll();
        list.add(node.val);
        if (node.left != null) queue.add(node.left);
        if (node.right != null) queue.add(node.right);
    }
    int[] res = new int[list.size()];
    for(int i = 0; i < list.size(); i++){
        res[i] = list.get(i);
    }
    return res;
}

2.

//从上到下打印二叉树，每一层打印一行
//用一个临时数组表示当前层的节点
public List<List<Integer>> levelOrder2(TreeNode root) {
    if (root == null) return new ArrayList<>();
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    LinkedList<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        List<Integer> tmp = new ArrayList<>();
        for(int i = queue.size(); i >0; i--){//将这一层节点子节点加入到队列中.出队固定长度
            TreeNode node = queue.poll();
            tmp.add(node.val);
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        res.add(tmp);
    }
    return res;
}

3.

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

//请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。
//使用双端队列
public List<List<Integer>> levelOrder3(TreeNode root) {
    if (root == null) return new ArrayList<>();
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    LinkedList<TreeNode> queue = new LinkedList<>();
    boolean flag = false; //false左向右打印，true反向打印
    queue.add(root);
    while (!queue.isEmpty()){
        LinkedList<Integer> tmp = new LinkedList<>();
        for(int i = queue.size(); i >0; i--){//将这一层节点子节点加入到队列中.出队固定长度
            TreeNode node = queue.poll();
            if (res.size()%2==0) tmp.addLast(node.val); //偶数层 队列尾部
            else tmp.addFirst(node.val);//奇数层，队列头部
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        res.add(tmp);
    }
    return res;
}

33 二叉搜索树的后序遍历的

后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。
二叉搜索树定义：左子树中所有节点的值 <<根节点的值；右子树中所有节点的值 > 根节点的值；其左、右子树也分别为二叉搜索树。

递归分治

根据二叉搜索树的定义，可以通过递归，判断所有子树的正确性（即其后序遍历是否满足二叉搜索树的定义），若所有子树都正确，则此序列为二叉搜索树的后序遍历。

终止条件：当i≥j ，说明此子树节点数量≤1 ，无需判别正确性，因此直接返回 true ；
递推工作：
1. 划分左右子树：遍历后序遍历的 [i, j] 区间元素，寻找 第一个大于根节点的节点，索引记为 m 。此时，可划分出左子树区间 [i,m-1]、右子树区间 [m, j - 1]、根节点索引 j 。
2. 判断是否为二叉搜索树：
  左子树区间 [i, m - 1]内的所有节点都应 < postorder[j]。而第 1.划分左右子树步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
  右子树区间 [m, j-1]内的所有节点都应 > postorder[j]。实现方式为遍历，当遇到 ≤postorder[j] 的节点则跳出；则可通过 p = j判断是否为二叉搜索树。
返回值：所有子树都需正确才可判定正确，因此使用与逻辑符 &&&& 连接。
p = j：判断此树是否正确。
recur(i, m - 1)：判断此树的左子树是否正确。
recur(m, j - 1 )：判断此树的右子树是否正确。

public boolean verifyPostorder(int[] postorder) {
    return recur(postorder,0,postorder.length-1); //第一棵树从根节点开始
}

private boolean recur(int[] postorder, int i, int j) {
    if (i>j){ //遍历完这棵树
        return true;
    }
    int p=i;
    while (postorder[p]<postorder[j]) p++; //找到第一个小于根节点的值的节点 ，划分左右
    int m = p; //索引
    while (postorder[p]>postorder[j]) p++; //检查右子树是不是小于
    return p == j && recur(postorder,i,m-1) && recur(postorder,m,j-1);
}

JZ35 二叉树中值为某一值的路径

LinkedList<List<Integer>> res = new LinkedList<>(); //返回值结果
LinkedList<Integer> tmp = new LinkedList<>();  //临时变量
public List<List<Integer>> pathSum(TreeNode root, int sum) {
    recur(root,sum);
    return res;
}

/**
 *节点为null直接返回
 * @param node 当前节点
 * @param sum 当前计算值
 */
void recur(TreeNode node, int sum){
    if(node == null) return;
    tmp.add(node.val);
    sum = sum - node.val;

    if (sum == 0 && node.left == null && node.right == null){ //sum为0并且左右节点为null
        res.add(new LinkedList<>(tmp)); //新的
    }
    recur(node.left,sum);  //左节点
    recur(node.right,sum);  //右节点
    //回溯
    tmp.removeLast();
}

JZ35 复杂链表的复制

利用hashmap来存储数据key是旧的值，value是新的值，通过旧值来构造一个新的值

public Node copyRandomList(Node head) {

    Node node = head;
    HashMap<Node,Node> map = new HashMap();
    while (node != null){
        map.put(node,new Node(node.val));
        node = node.next;
    }
    node = head;
    while (node != null){
        map.get(node).next = map.get(node.next);
        map.get(node).random = map.get(node.random);
        node = node.next;
    }
    return map.get(head);
}

JZ36 二叉搜索树与双向链表

输入一颗二叉搜索树将它转化成一个双向链表。

排序链表：利用”中序遍历“从小到大访问树的节点
双向链表：在构建相邻节点（前驱pre,当前节点cur）,pre.right = cur也应cur.left = pre.
循环链表：head.left = tail 和tail.right = head

public class JZ36 {
    Node pre,head;
    public Node treeToDoublyList(Node root) {
        if (root == null) return null;
        dfs(root);//递归成为一个
        head.left = pre; //将头结点和尾结点连接起来
        pre.right = head;
        return head;
    }
    //深度遍历
    public void dfs(Node cur){
        if (cur == null) return;
        dfs(cur.left);
        if (pre != null) pre.right = cur; //不是第一个节点，就对讲节点进行连接
        else head = cur;                //是第一个节点就将head指向这个节点
        cur.left = pre; //两个节点连接起来
        pre = cur;
        dfs(cur.right);
    }
}

JZ37 序列化和反序列化

实现序列化和反序列化

public String serialize(TreeNode root) {
    if(root == null) return "[]";
    StringBuilder res = new StringBuilder("[");
    Queue<TreeNode> queue = new LinkedList<TreeNode>() {{ add(root); }};
    while(!queue.isEmpty()) {
        TreeNode node = queue.poll();
        if(node != null) {
            res.append(node.val + ",");
            queue.add(node.left);
            queue.add(node.right);
        }
        else res.append("null,");
    }
    res.deleteCharAt(res.length() - 1);
    res.append("]");
    return res.toString();
}

public TreeNode deserialize(String data) {
    if(data.equals("[]")) return null;
    String[] vals = data.substring(1, data.length() - 1).split(",");
    TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
    Queue<TreeNode> queue = new LinkedList<TreeNode>() {{ add(root); }};
    int i = 1;
    while(!queue.isEmpty()) {
        TreeNode node = queue.poll();
        if(!vals[i].equals("null")) {
            node.left = new TreeNode(Integer.parseInt(vals[i]));
            queue.add(node.left);
        }
        i++;
        if(!vals[i].equals("null")) {
            node.right = new TreeNode(Integer.parseInt(vals[i]));
            queue.add(node.right);
        }
        i++;
    }
    return root;
}