解决的问题

字符串中最长回文子串的长度如何求解？

如何做到时间复杂度O(n)完成？

例如：abc1 232 0del 最长回文子串为232。

经典解法

将每个字符从中间开始向两边扩展可以得到最长回文子串吗？不能。

因为只能得到奇数的回文子串。 例如：1221。

上面只处理了实轴，我们加入虚轴。将字符串中每个字符中间加入特殊符号，如#，得到扩充字符，再使用上面的解法就可以得到答案。

例如：

将1221扩充为： #1#2#2#1，从每个字符向两边扩展，得到每个字符的最长回文串，最中间#的为9，除2,得到最长回文子串为4。

但是，加入的字符必须是没有出现的字符吗？不需要，每次处理字符串都是实轴和实轴比，虚轴和虚轴比，1和1比，#和#比。

经典解法的时间复杂度O(n)

Manacher解法

概念

回文直径和回文半径，回文直径是一个位置向2边扩的长度叫回文直径，一半是回文半径。

回文串的最右边界：，只要突破边界，就记录突破的位置。#1#2#2#1 对于第1个字符1来说是0-2，就是2；对于对于第3个字符2来说是2-4就更新为4；对于第4个字符#是0-8。

取得更远边界时中心点：对于第1个字符1来说是0-2，中心点是1；对于对于的3个字符2来说是2-4，中心点就是3；对于第4个字符#是0-8，中心点为4。

原理

解法

  1. 暴力扩，如果i位置没有在最右回文右边界只能暴力计算。

  2. 如果i位置在最右回文右边界，中心点C在i的左侧。i_mirror的回文区域与i位置的回文区域成逆序关系。设C的回文半径为[L-R]。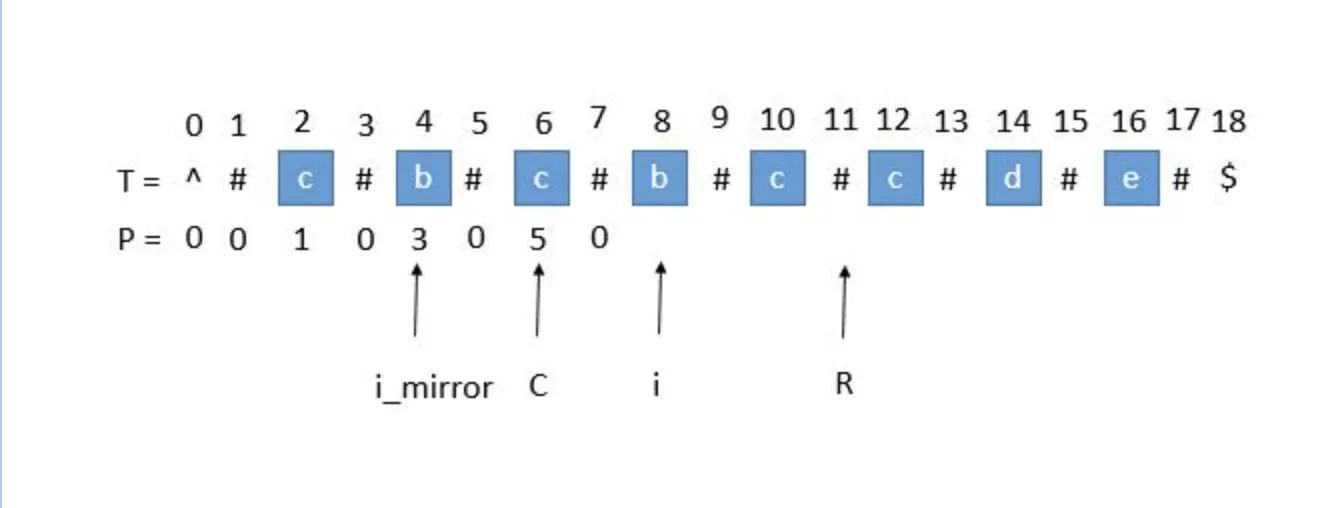

    img

    • i_mirror位置的回文半径在[L-R]中, P[i] = P[i_mirror]

    • i_mirror位置的回文半径超出[L-R]: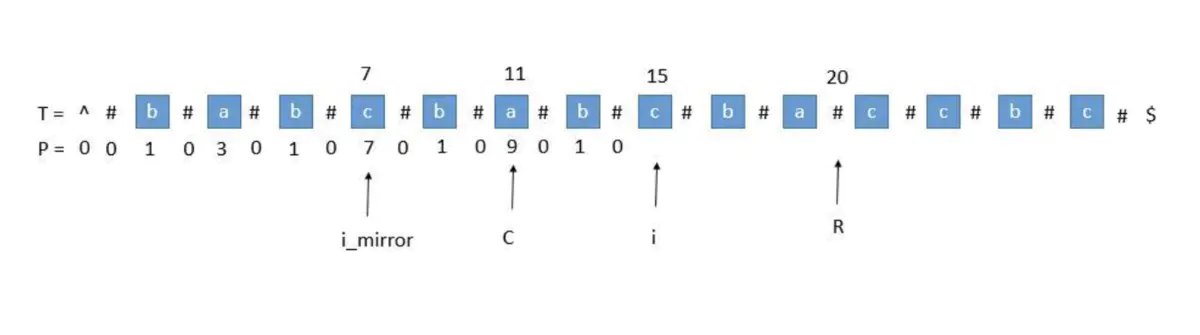

      img

      P[i_mirror] = 7, 但是我们发现此时 P [ i ] 并不等于 7 ，为什么呢，因为我们从 i 开始往后数 7 个，等于 22 ，已经超过了最右的 R ，此时不能利用对称性了，但我们一定可以扩展到 R 的，所以 P [ i ] 至少等于 R - i = 20 - 15 = 5，会不会更大呢，我们只需要比较 T [ R+1 ] 和 T [ R+1 ]关于 i 的对称点就行了，就像中心扩展法一样一个个扩展。

    • P [ i_mirror ] 遇到了原字符串的左边界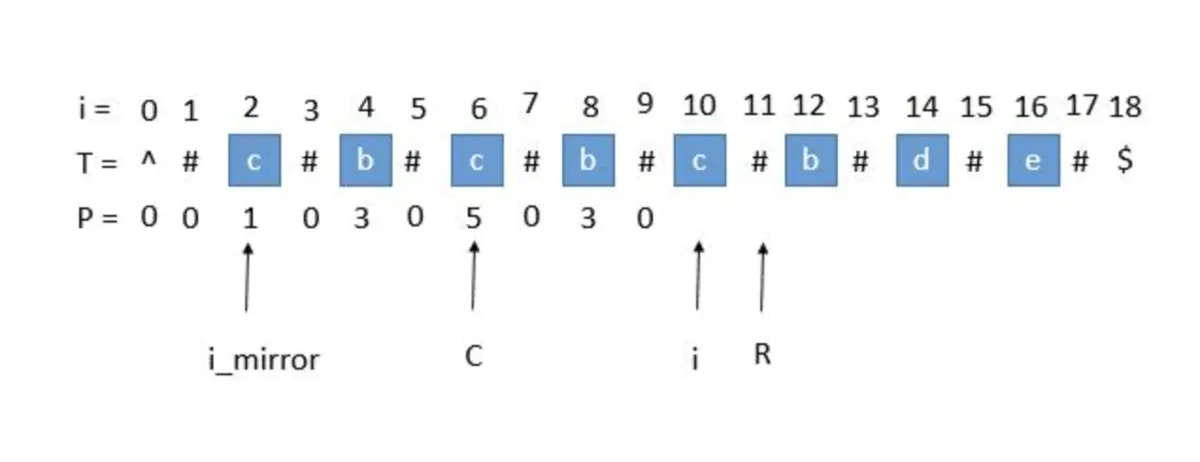

      img

      此时P [ i_mirror ] = 1，但是 P [ i ] 赋值成 1 是不正确的，出现这种情况的原因是 P [ i_mirror ] 在扩展的时候首先是 “#” == “#” ，之后遇到了 “^”和另一个字符比较，也就是到了边界，才终止循环的。而 P [ i ] 并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class Manacher {

    public static char[] manacherString(String s) {
        // 1221 -> #1#2#2#1
        char[] charArr = s.toCharArray();
        char[] res = new char[s.length() * 2 + 1];
        int index = 0;
        for (int i = 0; i < res.length; i++) {
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }

    public static int maxLcpsLength(String s) {
        if (s == null || s.length() == 0) {
            return 0;
        }

        char[] str = manacherString(s);
        int[] pArr = new int[str.length]; //回文半径数组
        int C = -1; // 中心
        int R = -1; // 回文右边界再往右一个位置，有效区是R-1位置
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < str.length; i++) {      //每个位置求回文半径
            // i至少的回文区域。
            // i在R外 1
            // i在R内 pArr[2 * C - i]， R - i中最小的 P[i_mirror], R-i 镜像的位置和i到R的位置谁小。3种情况
            // P[i_mirror]在R内 取 P[i_mirror]
            // P[i_mirror]在R外，或到达边界 取 R-i
            pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;

            // 如果没有超过str的长度，并且该位置可以扩
            while (i + pArr[i] < str.length && i - pArr[i] > -1) {
                // 跳过不用比的区域，看能不能扩的更大
                if (str[i + pArr[i]] == str[i - pArr[i]]) {
                    pArr[i]++;
                } else { //不能扩大，pArr[i]就是当前的最大位置
                    break;
                }
            }

            if (i + pArr[i] > R) { // 如果该位置回文串比之前的位置大
                R = i + pArr[i]; // 更新回文右边界
                C = i;  // 更新中心
            }
            max = Math.max(max, pArr[i]); // 记录最大回文半径
        }

        return max -1; // 原始串的最大回文长度
    }

    public static void main(String[] args) {
        System.out.println(Manacher.maxLcpsLength("ababa"));
    }

}

参考：

https://www.jianshu.com/p/b7152d81d579