有序表
有序表是一种查找时间复杂度为O(logn)的算法,实现有序表的情况有红黑树、AVL树、SB树、跳表。
前3个都属于平衡搜索二叉树系列BST
如果我们有一个搜索二叉树,如何能让他的增删改查就尽量快一些。一般默认搜索二叉树没有重复节点,因为我们可以通过增数据项存重述节点的信息。就是一个节点的信息多一些,也不重要。在搜索二叉树中进行操作增删改查的操作,但是因为不平衡,所以我们是不能保证时间复杂度。一旦不平衡,我们的时间复杂度可能就是O(N)。所以我们要保证平衡性。
AVL树
AVL树:是最最严格的平衡树,它每一个节点,左右子树高度差不超过一
为了满足这个操作,需要引入两个操作:左旋+右旋。旋转表示的是头结点往哪边倒。
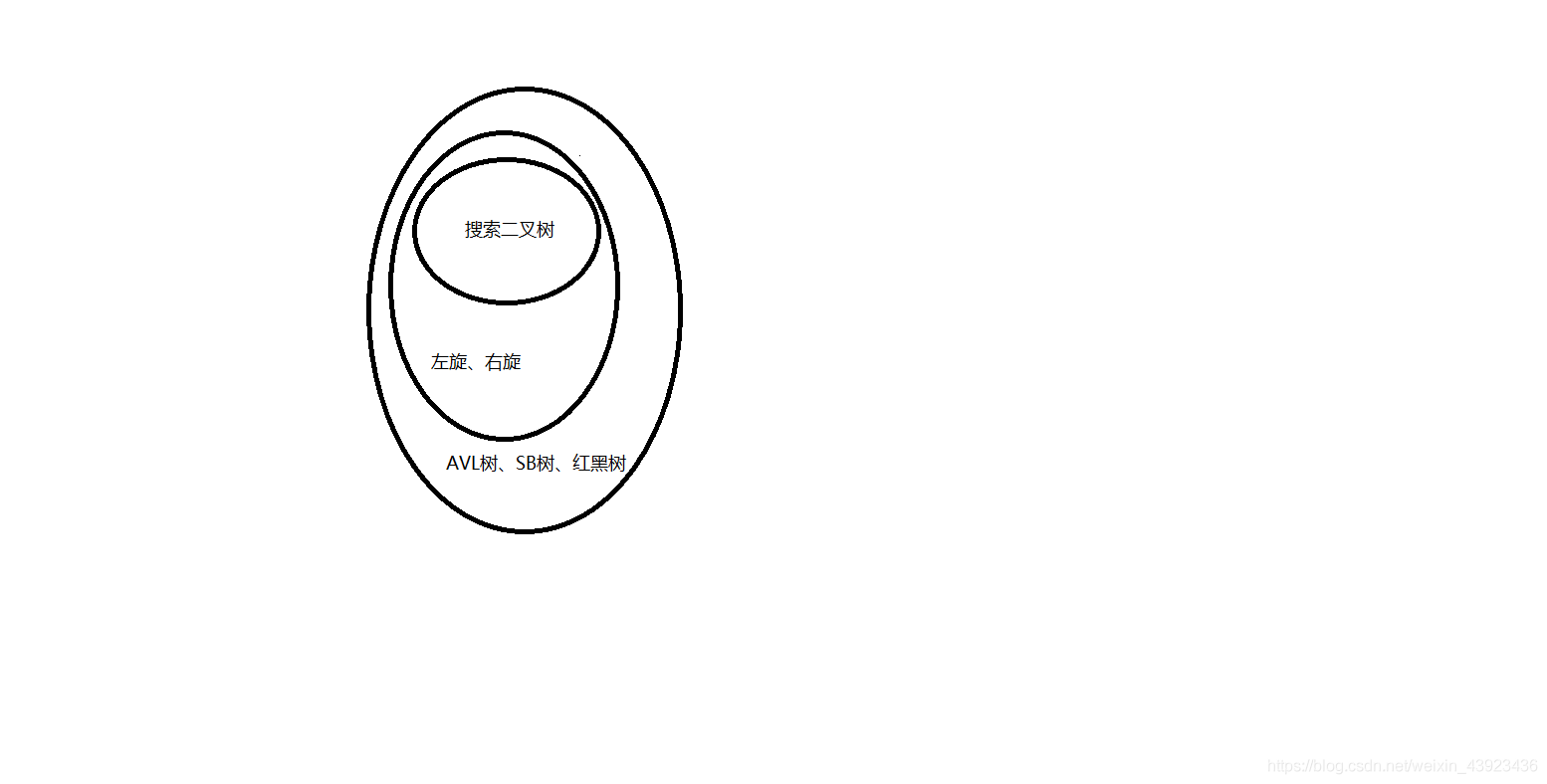
AVL树实现的是怎么用左旋和右旋的操作;红黑树也是实现左旋和右旋,并且有自己关于平衡的定义;SB树同样也有自己平衡的操作。
AVL树是怎么发现自己不平衡的?
AVL数的增删改查与搜索二叉树相同,只是在增加节点后,会从当前增加的节点开始向上查找是否有平衡性;对于删除来说,是从替换节点(一个节点删除必然有节点替换这个节点)开始查找是否有平衡性。
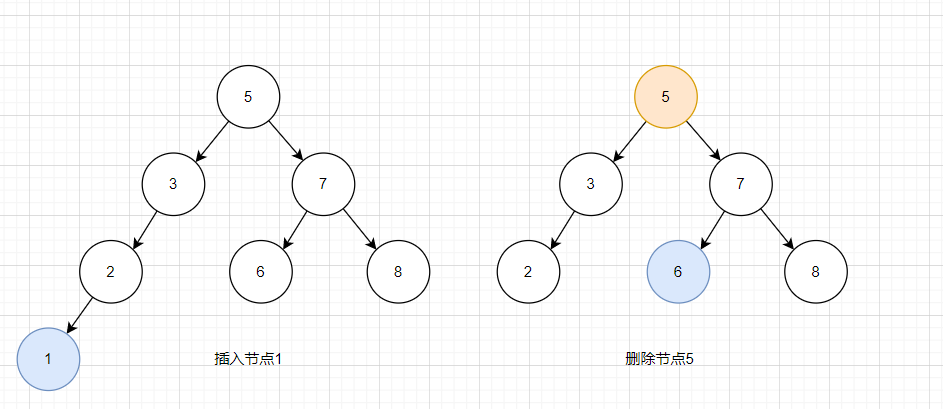
对于插入节点1来说,就从插入节点1开始向上查看每个节点是否平衡;对于删除节点5来说,会从它的替换节点6的上一个节点7开始查看每个节点是否不平衡
平衡性被破坏的情况
AVL树有4 种类别进行固定化程序的操作。
LL右单旋
LL的意思是向左子树(L)的左孩子(L)中插入新节点后导致不平衡,这种情况下需要右旋操作,而不是说LL的意思是右旋,后面的也是一样。我们需要对节点y进行平衡的维护。
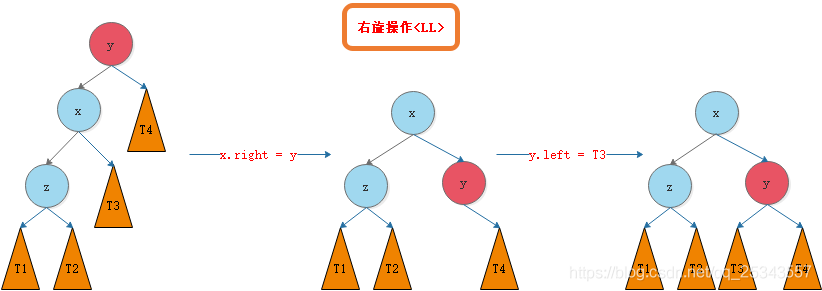
RR左单旋
我们需要对节点y进行平衡的维护。
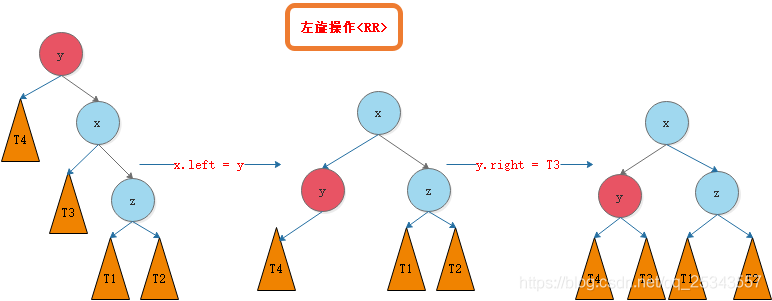
LR先左旋后右旋
节点插入左子树(L)的右子树(R)中
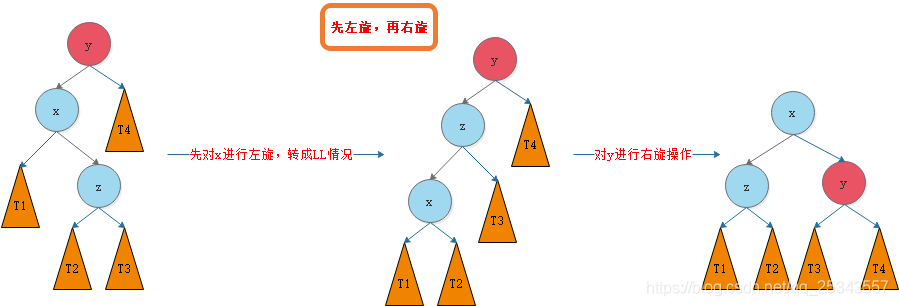
第三个图中x和z反了,失误
RL先右旋后左旋
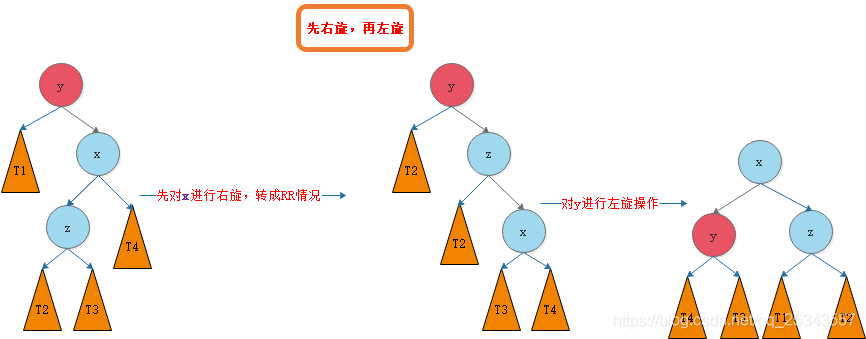
第二个图中y的左孩子为T1,第三个图中x和z反了,孩子也错了,应该是从左至右T1,T2,T3,T4,失误。。。
(红黑树和SB树)与AVL树的区别只在于和AVL的节点平衡性判定标准不一样,别的都一样。处理平衡的方式也是左右旋。
AVL数维持的是高度信息,红黑树维持的是自己关于平衡的信息,SB树维持的是有多少个节点的信息。平衡树在更新时保证把信息更新对。
SB树
平衡标准
每棵子树的节点个数,不小于其兄弟的子树的节点个数
既每棵叔叔树的节点个数,不小于其任何侄子树的节点个数
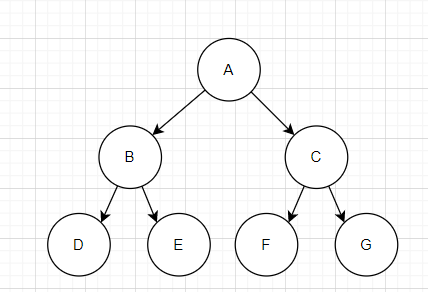
[B] >= max{[F],[G]}, [C]>=max{[D],[E]}
Size-Balance树也是有四种不平衡情况:
LL,LR,RL,RR
红黑树
平衡标准
- 每个节点都是红色,或黑色。
- 根节点是黑色。
- 每个叶子节点(最底层的空区域,没有数据)是黑色。
- 如果一个节点是红色,它儿子节点都是黑色(红节点不能相邻)。
- 对每个节点,从该节点到子孙节点的所有路径上包含相同数目的黑节点。
从头到底的路径最长的路径是红黑节点交替的路径,从头到底的路径最短的路径是只有黑节点,而到达底部黑色节点相同,那么这2条路径的差距就是2倍。红黑树要表达的是路径关系。
跳表
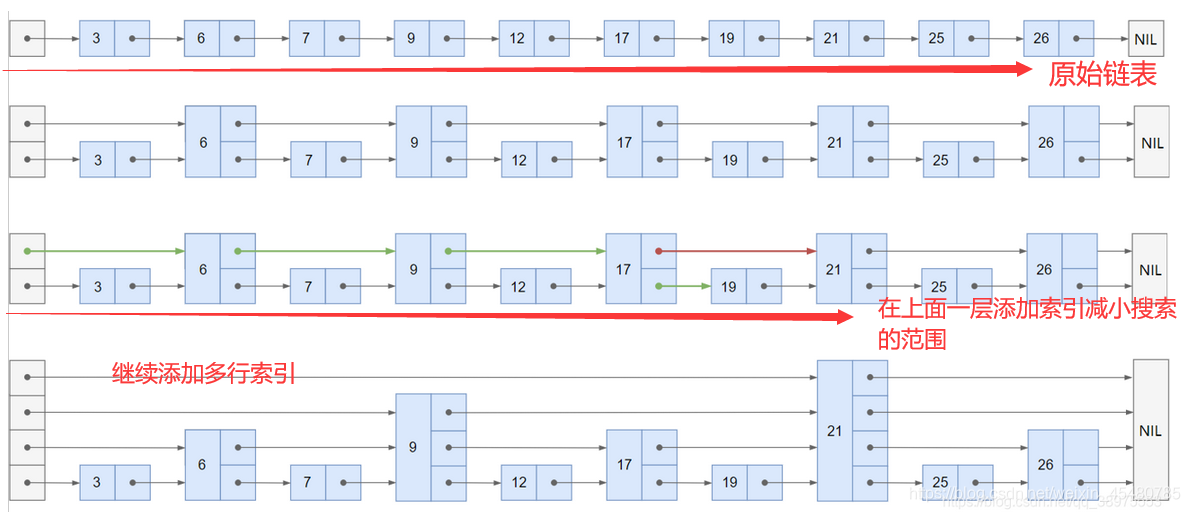
- 跳表,又叫做跳跃表、跳跃列表,在有序链表的基础上增加了“跳跃”的功能
- 跳表在原来的有序链表上加上了多级索引,通过索引来快速查找;可以支持快速的删除、插入和查找操作。
- 跳表实际上是一种增加了前向指针的链表,是一种随机化的数据结构
- Redis中 的
SortedSet、LevelDB中的MemTable都用到了跳表 - 对比平衡树, 跳表的实现和维护会更加简单, 跳表的搜索、删除、添加的平均时间复杂度是
O(logn)
增删改查
搜索
- 从顶层链表的首元素开始,从左往右搜索,直至找到一个大于或等于目标的元素,或者到达当前层链表的尾部
- 如果该元素等于目标元素,则表明该元素已被找到
- 如果该元素大于目标元素或已到达链表的尾部,则退回到当前层的前一个元素,然后转入下一层进行搜索
插入
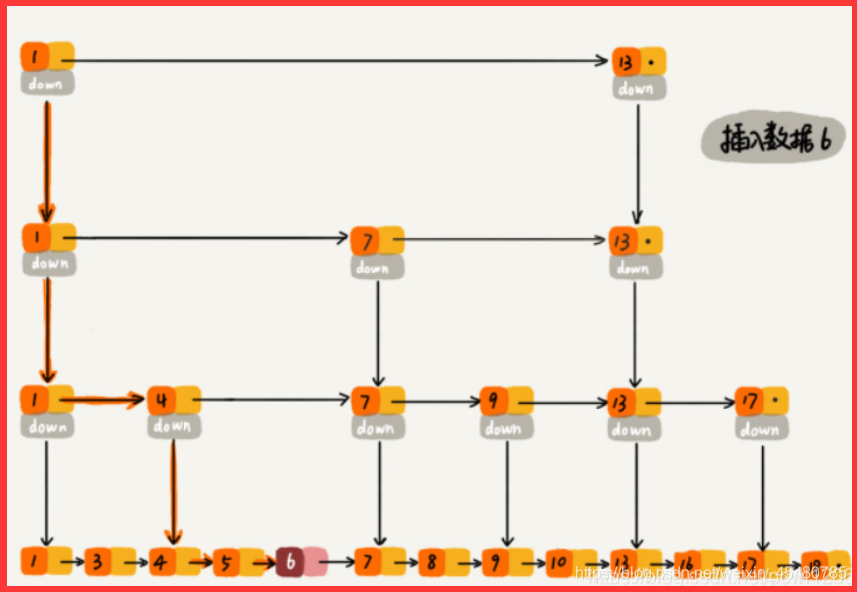
删除
在跳表中删除某个结点时,如果这个结点在索引中也出现了,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到删除结点的前驱结点,然后再通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点(双向链表除外)。因此跳表的删除操作时间复杂度即为O(logn)。
索引动态更新
当我们不断地往跳表中插入数据时,我们如果不更新索引,就有可能出现某2个索引节点之间的数据非常多的情况,在极端情况下,跳表还会退化成单链表
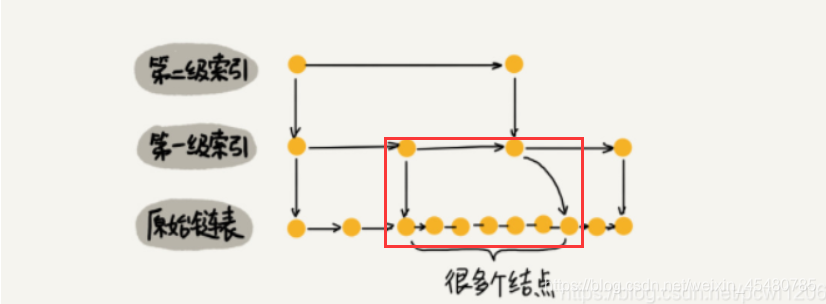
跳表是通过随机函数来维护“平衡性”。
当我们在跳表中插入数据的时候,我们通过选择同时将这个数据插入到部分索引层中,如何选择索引层,可以通过一个随机函数来决定这个节点插入到哪几级索引中,比如随机生成了k,那么就将这个索引加入到,第一级到第k级索引中。
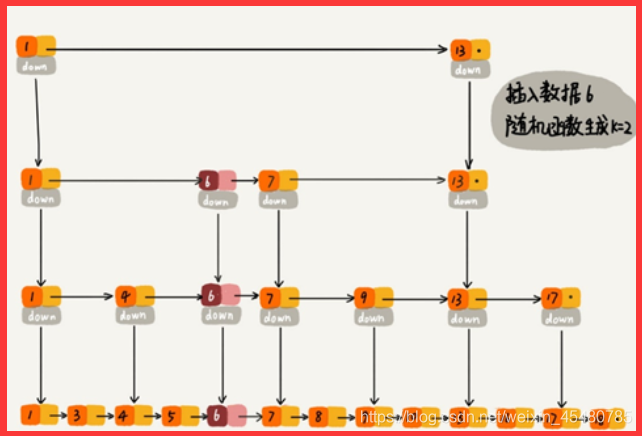
性质
- 跳表由很多层结构组成,level是通过一定的概率随机产生的;
- 每一层都是一个有序的链表,默认是升序 ;
- 最底层(Level 1)的链表包含所有元素;
- 如果一个元素出现在Level i 的链表中,则它在Level i 之下的链表也都会出现;
- 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
参考
[详细图文——AVL树][https://blog.csdn.net/qq_25343557/article/details/89110319]
[跳表(Skip List)][https://blog.csdn.net/weixin_45480785/article/details/116293416]





